Fun with Morphing

In my first post I mentioned that Thompson anticipated the developing of image morphing. Just for fun I decided to explore the application of morphing programs to Thompson’s images. I googled morphing software and looked at a few of the many offerings, some free, some not. One nice-looking non-free option is Fantamorph, which has a gallery of their own and customers creations, some quite impressive. Several are relevant to the topic of this blog:

For my experiment in Thomson-inspired morphing, I chose two images at random:

First I thought I'd better check to make sure Thompson hadn't “cooked the books” by misrepresenting their shapes. I googled up some images of Polyprion (a.k.a Atlantic wreckfish) and Scorpaena; he appears to have done them justice, though perhaps exaggerated the differences a bit:

Not wanting to spend any money on the exercise, I downloaded Free Morphing, which was fairly simple to learn. You place lines on one image, reposition them in the second, and it then interpolates between them.

I tried it on the images I had pulled up. Not surprisingly, it did something reasonable with the two fish. I wanted to put a video of it into the blog, but it didn't save in any blog-ready formats, so I needed some additional software. I found CamStudio which lets you capture screen events as video. The result is below (click triangle to play):

 

Of course, we already knew that you could morph shapes as disparate as Professor McGonagall and a cat into each other, so the "success" of this little experiment tells us nothing of interest scientifically. Furthermore, the program does not present us with an explicit grid describing the deformation, so we cannot even tell if the deformation looks like Thompson’s. 
To address this I tried another approach, which was to morph the grid and carry the fish along for the ride; that also produced plausible looking results:

Hower, as before, it doesn’t really demonstrate anything. The problem is, with morphing I  always end up at my target image, there is no suspense. It doesn't let me evaluate whether some transformation will get me there; it gives a tranformation that does. It would be nice to be able to define a transformation, say as a grid distortion; apply it to fish A, and then compare the resulting distorted fish A' to fish B to see how well they match. Maybe next time I'll try PhotoShop...
What this exercise did clarify for me is that a critical point of Thompson’s transformation images is that the deformations be in some sense simple, or regular. In mathematical terms this means it should be possible to describe them with few parameters (numbers). If I allow every point of interest in image A to move to an arbitrary new position in image B, I could describe the transformation with 2*n numbers (x,y displacements of each point), where n is the number of points (called fiducial points in the trade). For a fish, I could probably get by with n on the order of 10 or so fiducial points, so with 20 numbers I could get as cubist as I wanted. To the extent that the deformation is regular, I should be able to get by with many fewer numbers than that. I can describe a scaling transformation with just one number, a scale factor; for a two-dimensional rotation or shear I might need 4.
 
How many numbers do I need to describe Thompson's transformations? Closer to 1 or to 20?  Thompson’s diagrams seem to be saying look how regular Nature’s transformations are! But is it true? Certainly growth is fairly regular, unless you have teenage children. It is not a simple zoom (or dilation or scaling) transformation, because some aspects of the organism scale according to different powers of the overall size. For example, the weight of an organism is proportional to its volume, and so scales as the cube of its overall size, but the compression strength of bone is proportional to its cross-sectional area, and so scales as the square of the linear dimensions. This means that if you simply scale a cat to the size of a lion, its bones will be too thin for its weight, and they will fracture. To compensate, bones have to get thicker faster as the body grows. This general principle is called allometric scaling, and has been known for a long time.

Thompson’s transformations are not so much about growth, however, but about form; not the ontogenic transformations but the phylogenetic. Are the deformations between related species describable with few parameters, and if so, is that interesting? Maybe all this time these transformations have been some kind of conjurer’s trick, a clever iconic image with no real significance. How many parameters would I need to describe the warping of Polyprion into Scorpaena? The horizontal lines get squished towards the back; one number could probably describe the extent of the squishing. Thompson curves the verticals, which would burn extra parameters, since curves are mathematically more expensive to describe than lines. However, I didn't curve them, since curves are also more expensive to do in Free Morphing, which only gives you lines to work with; you would need to approximate a curve with a series of lines, which gets tedious rather quickly. However my lines seemed to work almost as well as Thompson's curves. So maybe you could turn Polyprion into Scorpaena with a few numbers. Some of Thompson's other transformations are more complex, and start to seem like special pleading.  Given that he lets himself choose from a rather open-ended family of tranformations, you would also technically require one or two parameters to specify the type of transformation; it starts to look like an exercise in minimum length encoding or Kolmogorov complexity, i.e., the shortest way to describe something complicated.

If we accept the point that many morphological transformations between species are simple in the sense of being describable with a small number of parameters, is this biologically interesting? After all, Nature is not using a warping algorithm or specifying parameters. Or is She? The transcription factors mentioned in the last post, the regulators of genes, bind with a strength determined by the sequence of the DNA they are binding to. Change the sequence, change the binding strength, change how hard this regulator turns that gene on or off, and therefore change, or modulate, all the downstream effects of that gene. If that gene says grow the front, or the back, of the critter this much, then you change the shape. So maybe there's something here after all...

Circuit Diagram for a Sea Urchin

Fast-forward 80 or so years from the publication of On Growth and Form in 1917 to the mid-1990’s, pausing for a brief nod to the stunning accomplishments of molecular biology in the last half of the 20th century. These include, first and foremost, the unraveling of the structure of DNA, with its moment of drama unmatched in the history of science, so well described in Horace Judson’s 8th Day of Creation, when the structure suddenly fell into place like a jigsaw puzzle. “We have discovered the secret of life” they told the waiter at the Eagle pub. The discovery was an announced to the world in a 1 page paper legendary for both its brevity and its understated conclusion: “It has not escaped our notice that the specific pairing we have postulated immediately suggests a possible copying mechanism for the genetic material.”.

Their discovery launched a decade or so of working out the genetic code and the machinery of what has become known as the Central Dogma of molecular biology: DNA makes DNA, and also DNA makes (messenger) RNA, which makes proteins, which drive the symphony of organized chemistry we call life. These insights launched a thousand successive revolutions both pure and applied, including recombinant DNA technology, the biotechnology industry, “biologic” drugs (i.e., therapeutic proteins), gene therapy (not yet ready for prime time), and the era of genome sequencing epitomized by, but by no means limited to, the sequencing of the human genome. The simplicity of the central dogma has been under assault in the last decade, as RNA has refused to be content with the messenger role assigned to it, and has been laying claim to previously unsuspected new functions, from chemical catalysis to gene regulation. But I am getting ahead of myself. By the mid-1990’s the central dogma was settled, a couple of decades of painstaking piecemeal sequencing of isolated genes had passed, and high throughput sequencing was ramping up, so that one knew that it was a matter of time before complete gene lists for organisms would start to become available.



Genes were (are) thought to be the atomic statements, the single lines of code, in the organismal program. People’s thoughts were turning increasingly to gene regulation, the mechanism which tells a cell which genes to turn on when, and hence which proteins to make. Gene regulation itself was not a new concept; it has its own august history going back to the pioneering work of Jacob and Monod in the early 1960’s with the unraveling of the first bacterial operon. However, with the industrialization of sequencing bringing with it the prospect of complete knowledge of genome sequence, the possibility of a complete understanding of gene regulatory programs was now starting to become less far-fetched.


With that setting of the historical stage, I want to turn to a 1996 paper in the journal Development by Eric Davidson and his student Chiow Hwa Yuh entitled Modular cis-regulatory organization of Endo16, a gut-specific gene of the sea urchin embryo . Davidson, a professor of developmental biology at CalTech, had by this time spent several decades studying the early development of the sea urchin. Why the sea urchin, you might ask? Well, since you asked, allow me one more digression on the subject of model organisms. While much biological research is justified in grant proposals by its potential impact on practical goals like advancing human health or agricultural productivity, it turns out that people and corn, respectively, are often not the most convenient organisms to do experiments in. The factors that make an organism convenient for experimentation include ease and cost of propagation in a laboratory, a short generation time to allow the effects of mutations or developmental perturbations to be observed quickly, and experimental tractability, which means a toolkit of methods and resources for tweaking the normal biology, usually amassed over a generation or two of research by a community of scientists focused on an organism. The worst possible organism for doing biology on is Homo sapiens: long generation time, tons of ethical restrictions on what sorts of experiments you can do, expensive to maintain, etc. In the plant world, the organisms we care most about, crops and trees, have generation times ranging from once per season for corn (2-3 generations per year if you are willing to switch back and forth between the northern and southern hemisphere, like agribusiness giants like Monsanto and DuPont/Pioneer), and once or twice per decade, for trees. Fortunately, a lot of biology is conserved across organisms, and you can learn a lot that is relevant to humans from studying organisms as far afield as yeast, which shares with us much fundamental machinery of cell division, to invertebrates like the sea urchin, the nematode worm or the fruitfly, which share with us many signaling, regulatory and developmental pathways, to nonmammalian vertebrates like the zebrafish, which shares many of our cell types and anatomical structures but has the tremendous advantage of being transparent, and closest to home, the mammalian model of choice, the mouse. For physiological research the rat enjoys some popularity, and dogs show considerable promise for teaching us about the genetics of behavior, but for molecular biology of development in mammals, the mouse is as good as it gets: fast, cheap and versatile. In the plant world the role of the mouse is played by the small, mustard-like weed Arapidopsis thaliana, extensively studied by plant geneticists, and the first plant to have its genome sequenced. The idea of having a simplified version of a complex system which can be more easily studied would seem to be fairly obvious, except that every few years some astonishingly ignorant politician will grab some headlines by complaining about taxpayer money being wasted on the study of fruitflies.



So: sea urchins. Like most multicellular organisms, they develop from a single cell. They go through early 2,4,8,… cell cleavages, passing through morula (raspberry), blastula (hollow ball) and gastrula (folded ball) phases of development similar to many other animal species, including ourselves. They are convenient: you can gather lots of fertilized eggs easily and watch them develop, or interfere. Davidson's lab studies the genetics of sea urchin development.

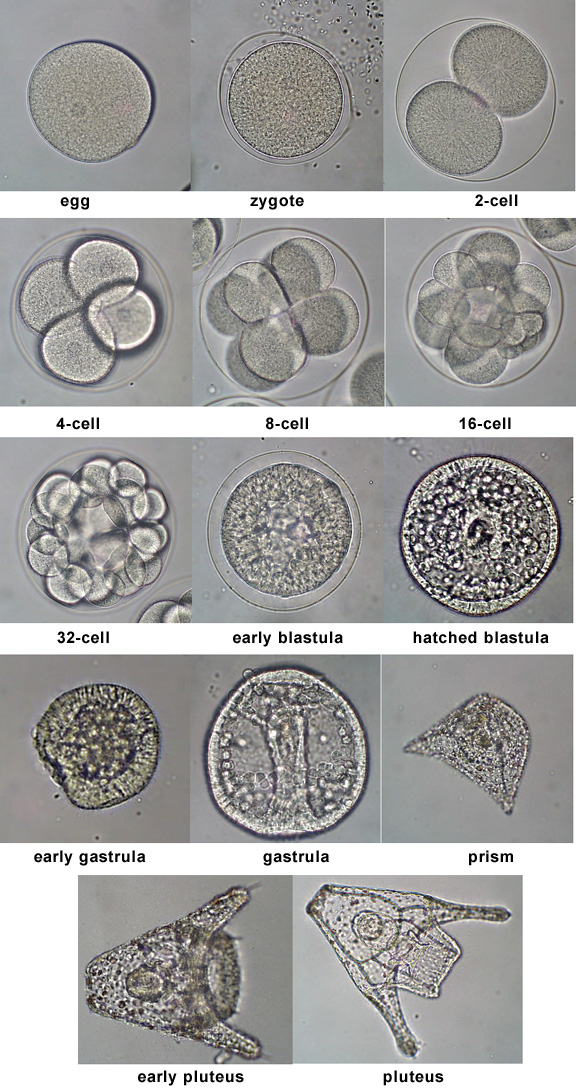The aforementioned 1996 paper presented a detailed model to explain the regulation of a single gene expressed in a particular tissue in a sea urchin embryo. The question was why there and then? One way genes are known to be regulated is via their promoters: DNA regions just upstream from the protein-coding part of the gene. Special proteins called transcription factors can recognize specific DNA sequences in the promoters of particular genes and bind to them; in so doing they can activate or repress the transcription of mRNA messages from that gene, which in one step in the chain leading to the manufacture of that gene's protein product. Different transcription factors recognize sequences in front of different genes, leading to a network of activation and repression relationships between genes and their protein products.



Yuh and Davidson's paper tried to work out a detailed model for the regulation of one gene: which transcription factors bound to its promoter and what the effect was. They had to do a lot of promoter bashing experiments to work this out. What was unusual about their paper was ttheir attempt to produce a complete, quasi-mathematical description of the activation conditions for the gene. They concluded that it was not enough to specify purely Boolean on/off conditions for the gene, although some of the transcription factors did have this kind of effect. Others had a more graded effect, with more bound proteins producing more gene expression.
You can see a summary here.

Above: a figure from the paper. See also a calculator to compute the model's output expression level under different conditions.

What was striking about their model was, first, how complex the regulation of one gene in one humble organism could be, but also the images suggested that the networks of gene regulation, while complex, might be amenable to the same sorts of diagrams and mathematics that electrical engineers use to make sense of complex circuits. In subsequent years Davidson and collaborators extended their models to include other genes, pathways, and species, and developed a set of diagramming conventions and tools for genetic regulatory networks (GRNs). Davidson later wrote Genomic Regulatory Systems

which is a manifesto for the unravelling of the regulatory networks of organisms. The GRN diagrams have been applied to a number of other species and systems. They have also grown considerably more complex:

From a Thompsonian perspective, this thread of work is incomplete in one crucial way. Although it provides a way of thinking about the control of genes, the work to date, to my knowledge, does not make the link to form. We still lack the simulator that can take the above diagram and compute a video of a developing sea-urchin embryo as output. That is no criticism of the work of Davidson and colleagues, who have taken us a huge step in that direction. Just an observation that there is a ways yet to go.

Blogging In Thompson's Footsteps

My fascination with the mathematics of biological form was first kindled by a childhood encounter with D’Arcy Thompson’s classic book On Growth and Form (henceforward oGaF). First published in 1917, this unique volume explores the intersection between biology and engineering mechanics. It is probably better known for its striking images than for its text, and for the questions it implicitly posed than for the answers it provided. This passage from a Wikipedia entry describes it nicely:

Utterly sui generis, the book never quite fit into the mainstream of biological thought. It does not really include a single unifying thesis, nor, in many cases, does it attempt to establish a causal relationship between the forms emerging from physics with the comparable forms seen in biology. It is a work in the "descriptive" tradition; Thompson did not articulate his insights in the form of experimental hypotheses that can be tested. Thompson was aware of this, saying that "This book of mine has little need of preface, for indeed it is 'all preface' from beginning to end."

The book is dense with curious facts about the connection between the Fibonacci series and the layout of seeds in sunflowers, or the ways in which simple inorganic processes can reproduce the shapes of jellyfish or the arrangement of cells in tissues. Thompson applied a mathematician’s eye to the shape of a ram’s horn and a chambered nautilus’ shell, and an engineer’s mind to the stresses and shapes in the skeletons of dinosaurs, birds and other creatures. But the most provocative part, the one responsible for the book’s continuing appeal, is the final chapter, entitled On the Theory of Transformations, or the Comparison of Related Forms. There Thompson investigates the relationship between the shapes of different species by imposing a regular mesh on one and then deforming it to match another – a device that anticipates the modern computational techniques of morphing and finite element analysis. The deformations seem regular, suggesting some deep hidden principle of morphological evolution.

And closer to home... The question elegantly posed by these images is: how does nature transform organism shapes in the course of evolution? This question depends on a still more basic one: how does nature generate organism forms in the first place? These questions are, respectively, the phylogenetic and ontogenic parts of the problem of morphogenesis.

Arguably oGaF was an anachronism, misplaced in time: a piece of 21st century biology accidentally dropped into the early 20th century, to paraphrase Edward Witten's comment about string theory. In order to get us to the point where we can begin to answer the questions implied by Thompson’s transformations, a set of distinct sciences and tools has had to be developed, each quite complex in their own right. These include molecular biology, genomics and evo devo; as well as the development of cheap computing power and computational methods of finite element analysis and computer graphics.

Nowadays, as biologists are starting to understand cells as metaphorical computers, we would say that the shape of an organism is a consequence of a “morphogenetic program” encoded in its genes and executed by its cells. Although many biologists believe this is correct in outline, we are still far from a detailed understanding of the complete morphogenetic program of any organism -- what Lewis Wolpert has called the computable embryo. However, in contrast to Thompson’s time, the foundations for that understanding are now in place, and one can reasonably predict that over the next few decades Thompson’s images will transition from tantalizing enigmas to icons of a new science of morphogenetics, encompassing genetics and mechanics, and utilizing computational modeling of morphogenesis as a fundamental tool.

The goal of this blog will be to assemble, as I have the time, bits of informational flotsam related to the goal of a full computational understanding of biological Growth and Form.